概统期末考点（LaTex试用）

随机事件及概率

• 条件概率——全概率公式+贝叶斯公式
• 古典概型

一维随机变量（离散型＋连续型）

• 离散型随机变量分布律/连续型随机变量概率密度
  • 概率密度$f(x)$
    • 分布函数<——> 概率密度的互推
    • 重难点（步骤）：求连续型变量$X$的函数$Y(X)$的分布函数和概率密度

二维随机变量（离散型+连布续型）

• 离散型随机变量联合分/边缘分布/条件分布（分布律）
• 连续型随机变量联合分布/边缘分布/条件分布（概率密度）
  • 最难点：两个连续型随机变量的函数的分布 $Z=X+Y$、$Z=XY$、$Z=\frac{X}{Y}$、$Z=\max\{X,Y\}...$
  • 独立性

随机变量的数字特征

• 数学期望$E(X)$
  • 离散型/连续型$E(X)$公式
  • 随机变量的函数的数学期望
    • 离散/连续
    • 一个随机变量/两个随机变量的函数
    • 期望的性质
• 方差$D(X)$
  • $D(X)与E(X)$的关系式
  • 标准化变量$X^* =\frac{X-\mu}\sigma{}$
  • 四个性质
  • 切比雪夫$\textit{(Chebyshev)}$不等式 $P\{|X-\mu| \geq \varepsilon\}\leq\frac{\sigma^2}{\varepsilon^2}$或$P\{|X-\mu| \leq \varepsilon\}\geq1-\frac{\sigma^2}{\varepsilon^2}$
• 协方差$\text{Cov}(X, Y)$、相关系数$\rho_{XY}$
  • 协方差
    • 定义式：$\text{Cov}(X,Y)=E\{[X-E(X)]^2[Y-E(Y)]^2\}$
    • 计算式：$\text{Cov}(X,Y) = E(XY)-E(X)E(Y)$
  • 相关系数
    • 定义：$\rho_{XY}=\frac{\text{Cov}(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$
    • 含义：$X、Y$相关程度 (仅就线性关系来说)
• 矩
  • 中心矩
  • 原点矩

大数定律和中心极限定理

• 辛钦大数定律 --> 伯努利大数定律
• 独立同分布的中心极限定理
• 李雅普诺夫$\textit{(Lyapunov)}$定理
• 棣莫弗-拉普拉斯$\textit{(De Moivre-Laplace)}$定理

样本及抽样分布

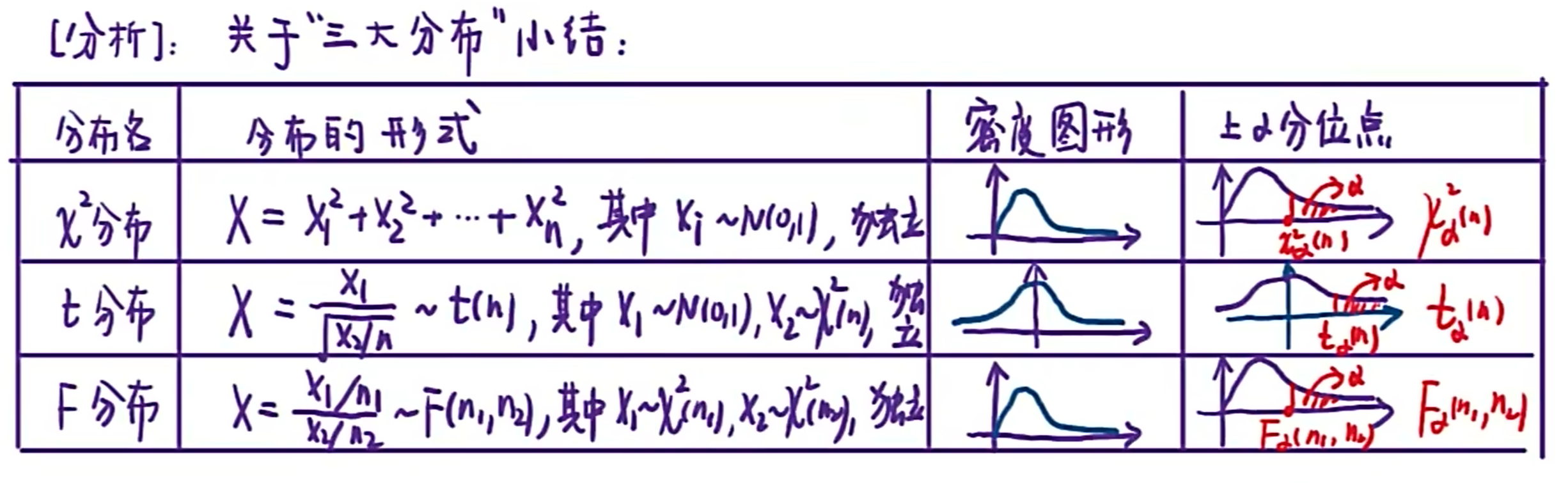
• 统计学三大分布
  • $\mathcal{X}^2$分布 $\mathcal{X}^2 \sim \mathcal{X}^2(n)$
    • $X$服从总体$N(0,1)$ --> 统计量$\mathcal{X}^2=X_1^2+X_2^2+ \cdots +X_n^2$
    • 可加性：$\mathcal{X_1}^2+\mathcal{X_2}^2 \sim \mathcal{X}^2(n_1+n_2)$
    • $E(\mathcal{X}^2)=n,D(\mathcal{X}^2)=2n$
  • $\text{t}$分布 $t \sim t(n)$
    • $X \sim N(0,1), Y \sim \mathcal{X}^2(n)$ --> 随机变量$t=\frac{X}{\sqrt{Y/n}}$
  • $F$分布 $F \sim F(n_1,n_2)$
    • $U \sim X^2(n_1),V \sim X^2(n_2)$ --> $F=\frac{U/n_1}{V/n_2}$

参数估计

• 点估计（估计量、估计值）
  • 矩估计：$n$充分大时，样本矩等于总体矩
    • 总体一阶矩$E(X)=$ 样本均值$\bar{X}$ --> 得到参数$\theta$的矩估计量$\hat{\theta}$
  • 最大似然估计：使得样本$x_1,x_2,\cdots,x_n$发生的概率最大的$\theta$值最恰当
    • 求似然函数$L(\theta)=L(x_1,x_2,\cdots,x_n;\theta)=\prod \limits_{i=1}^n p(x_i;\theta)$
    • 取对数$lnL(\theta)$
    • 求驻点得到$\hat{\theta}$
• 估计量的评选标准
  • 无偏性：$E(\hat\theta)=\theta$
  • 有效性：比较$D(\hat\theta)$
  • 相和性

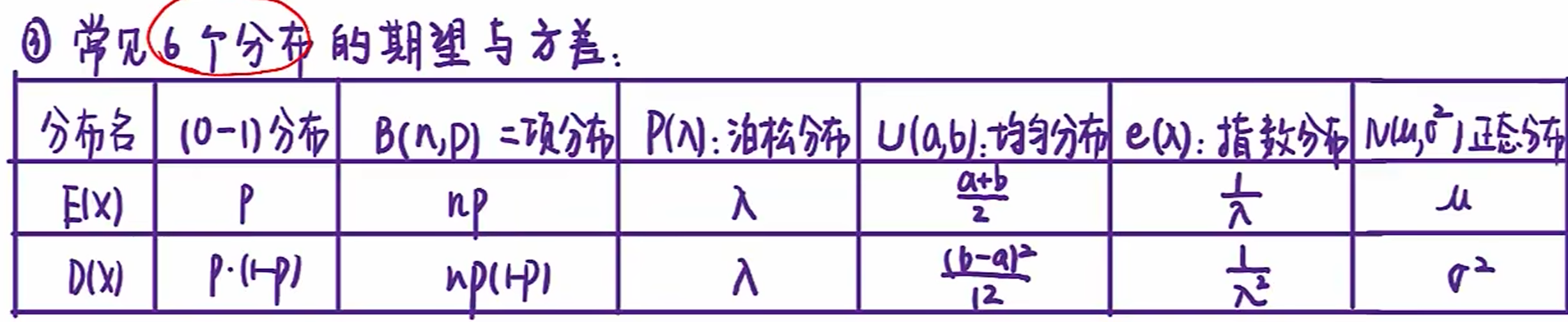
常见分布

• 二项分布 $X \sim \text{B}(n, p)$
  • $E=np$，$D=np(1-p)$
• 均匀分布 $X \sim \text{U}(a, b)$
• 正态分布 $X \sim \text{N}(\mu, \sigma^2)$
• 泊松分布 $X \sim \pi(\lambda)$
  • $E(X)=D(X)=\lambda$
• 指数分布$X \sim \text{e}(\theta)$
  • $E(X)=θ ，D(X)=θ^2$
• 几何分布$X \sim \text{Ge}(p)$
  • $E(X)=\frac{1}{p}$, $D(X)=\frac{1-p}{p^2}$